Wikipedia

Atoomorbitaal

In atoomteorie en kwantummeganika is 'n atoomorbitaal (of soms atoombaan of atoomwentelbaan) 'n wiskundige funksie wat die ligging en golfagtige gedrag van 'n elektron in 'n atoom beskryf.[1] Hierdie funksie kan gebruik word om die waarskynlikheid te bereken om enige elektron van 'n atoom in enige spesifieke streek rondom die atoomkern te vind. Die term atoomorbitaal kan ook verwys na die fisiese gebied of ruimte waar die elektron bereken kan word om te wees, soos voorspel deur die spesifieke wiskundige vorm van die orbitaal.[2]

Die vorms van die eerste vyf atoomorbitale is: 1s, 2s, 2px, 2py en 2pz. Die twee kleure toon die fase van die golffunksie in elke deel.

Elke wentelbaan in 'n atoom word gekenmerk deur 'n stel waardes van drie van die kwantumgetalle, naamlik elektronenergie (n), hoekmomentum (ℓ) en die magnetiese kwantumnommer (m). Elke orbitaal kan deur 'n maksimum van twee elektrone beset word, elk met sy eie spin-kwantumgetal (s). Die orbitale het eenvoudige name, s-orbitaal, p-orbitaal, d-orbitaal en f-orbitaal. Die name verwys na die hoekmomentum kwantumgetal, onderskeidelik ℓ = 0, 1, 2 en 3. Hierdie name, tesame met die waarde van n, word gebruik om die elektronkonfigurasies van atome te beskryf. Dit is afgelei van die vroeë beskrywing van sekere reekse van alkalimetaal-spektroskopiese lyne as skerp, prinsipieel, diffus en fundamenteel. Orbitale vir ℓ > 3 gaan alfabeties voort maar laat j weg (g, h, i , k , ... )[3][4][5] omdat sommige tale nie die letters " i " en "j" onderskei nie.[6]

Atoomorbitale is die basiese boustene van die atoombaanmodel (ook bekend as die elektronwolk- of golfmeganika-model), 'n moderne raamwerk om die submikroskopiese gedrag van elektrone in materie te visualiseer. In hierdie model kan die elektronwolk van 'n multi-elektronatoom by benadering gesien word as opgebou in 'n elektronkonfigurasie wat 'n produk is van eenvoudiger "waterstofagtige" atoomorbitale. Die herhalende periodisiteit van die blokke van 2, 6, 10 en 14 elemente binne gedeeltes van die periodieke tabel is natuurlik die gevolg van die totale aantal elektrone wat gevind word in 'n volledige stel van s, p, d en f atoomorbitale. Die orbitale behalwe s, dws. p, d, f, g, ens., kan verder opgebreek word in "suborbitale" wat tot 2 elektrone bevat. Die suborbitale word ook "sub-doppe" of "subskulpies" genoem.

Vir hoër waardes van die kwantumgetal n, veral wanneer die betrokke atoom 'n positiewe lading dra, word die energieë van sekere sub-orbitale baie dieselfde, en dus word die volgorder van bevolking van die elektrone in die orbitale deur gebruik van die Aufbau-beginsel ietwat willekeurig. Byvoorbeeld, die elektronkonfigurasie van Cr is [ Ar ]4s13d5 maar Cr2+ is [ Ar ]3d4. In die atoomfisika stem die atoomspektrale lyne ooreen met oorgange (kwantumspronge) tussen kwantumtoestande van 'n atoom. Hierdie toestande word gemerk deur 'n stel kwantumgetalle wat in die term simbool saamgevat word en gewoonlik geassosieer word met bepaalde elektronkonfigurasies, dws deur besettingskemas van atoomorbitale (byvoorbeeld 1s22s22p6 vir die grondtoestand van neon. Die grondtoestand het die simbool: 1S0).

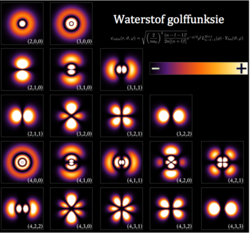
Atoomorbitale van die elektron in 'n waterstofatoom op verskillende energievlakke.

Einskappe van die elektron

wysig

Met die ontwikkeling van kwantummeganika en eksperimentele bevindings is gevind dat die wentelende elektrone om 'n kern nie volledig as deeltjies beskryf kan word nie, maar dat dit deur die golf-deeltjie-dualiteit verklaar moet word. In hierdie sin het die elektrone die volgende eienskappe:

Golfagtige eienskappe:

  1. Die elektrone wentel nie om die kern soos die planete om die son wentel nie, maar bestaan ​​eerder as staande golwe. Die laagste moontlike energie wat 'n elektron kan neem is dus soortgelyk aan die fundamentele frekwensie van 'n golf op 'n tou. Hoër energietoestande is soortgelyk aan harmonieke van daardie fundamentele frekwensie.
  2. Die elektrone is nooit op een punt geleë nie, alhoewel die waarskynlikheid om op 'n enkele punt met die elektron interaksie te hê, uit die golffunksie van die elektron gevind kan word. Die lading op die elektron werk asof dit in die ruimte uitgesmeer word in 'n deurlopende verspreiding, eweredig op enige punt met die kwadraat van die grote van die elektron se golffunksie.

Deeltjiesagtige eienskappe:

  1. Die aantal elektrone wat om die kern wentel, kan slegs 'n heelgetal wees.
  2. Elektrone spring soos deeltjies tussen orbitale. As 'n enkele foton byvoorbeeld die elektrone tref, verander slegs een elektron se toestand in reaksie op die foton.
  3. Die elektrone behou deeltjiesagtige eienskappe soos: elke golftoestand het dieselfde elektriese lading as sy elektrondeeltjie. Elke golftoestand het 'n enkele diskrete spin (spin op of spin af) afhangende van die kwantumsuperposisie daarvan.

Elektrone kan dus nie bloot as vaste deeltjies beskryf word nie. 'n Analogie is die van 'n groot en dikwels vreemd gevormde "atmosfeer" (die elektron) wat versprei is oor 'n relatief klein planeet (die atoomkern). Atoomorbitale beskryf die vorm van hierdie "atmosfeer" presies slegs wanneer 'n enkele elektron in 'n atoom voorkom. Wanneer meer elektrone by 'n enkele atoom gevoeg word, is die bykomende elektrone geneig om 'n eweredige hoeveelheid ruimte rondom die kern in te vul sodat die resulterende versameling (soms die "elektronwolk" genoem)[7] na 'n algemeen sferiese sone van waarskynlikheid neig, wat die ligging van die elektron beskryf, as gevolg van die onsekerheidsbeginsel.

Waterstof-, Slater- of Guasstipe orbitale

wysig
 
3D-aansigte van sommige waterstofagtige atoomorbitale wat waarskynlikheidsdigtheid en fase toon (g-orbitale en hoër word nie gewys nie)

Daar is drie wiskundige vergelykings wat gebruik word om die atoomorbitale voor te stel. Die eenvoudigste atoombaanvorme, gebaseer op die presiese oplossings van die Schrödinger-vergelyking vir 'n "waterstofagtige atoom", word in die onderrig gebruik. Gewysigde kombinasies van hierdie orbitale, genaamd Slater-tipe orbitale (STO)[8] word algemeen gebruik vir atome en diatomiese molekules. 'n Derde tipe, die Guassiese tipe,[9] word gebruik vir molekules met drie of meer atome, selfs al is hulle alleenweg nie so akkuraat as die STO's nie kan kombinasies van die Guassiese tipe die akkuraatheid van die "waterstofagtige" orbitale bereik.

Atoomorbitale word wiskundig in sferiese koördinate voorgestel as 'n funksie ψ(r, θ, φ) = R(r) Θ(θ) Φ(φ) wat 'n kombinasie van sferiese harmonieke Yℓm(θ, φ) is (waar ℓ en m kwantumgetalle is).

Geskiedenis

wysig
 
Deense fisikus Niels Bohr in 1922

Die term "orbitaal" is in 1932 deur Robert Mulliken geskep as 'n afkorting vir "een-elektron orbitale golffunksie".[10] Die idee dat elektrone dalk om 'n kompakte kern met 'n bepaalde hoekmomentum kan draai, is minstens 19 jaar vroeër oortuigend aangevoer deur Niels Bohr,[11] en die Japanse natuurkundige Hantaro Nagaoka het reeds in 1904 'n hipotese gebaseer op die gedrag van elektrone in 'n baan gepubliseer.[12] Die verduideliking van die gedrag van hierdie "elektronwentelbane" was een van die dryfkragte vir die ontwikkeling van kwantummeganika.[13]

Vroeë modelle

wysig

Met J.J. Thomson se ontdekking van die elektron in 1897,[14] het dit duidelik geword dat atome nie die kleinste boustene van die natuur is nie, maar eerder saamgestelde deeltjies. Die nuut ontdekte struktuur binne atome het baie mense laat bespiegel oor hoe die atoom se bestanddele met mekaar kon wissel. Thomson het geteoretiseer dat veelvuldige elektrone in wentelagtige ringe binne 'n positief gelaaide "jellie-agtige stof" draai,[15] en tussen die ontdekking van die elektron en 1909 was hierdie "pruimpuddingmodel" die mees aanvaarde verklaring van die atoomstruktuur.

Kort na Thomson se ontdekking het Hantaro Nagaoka 'n ander model vir elektroniese struktuur voorspel.[12] In teenstelling met die "pruimpoedingmodel", is die positiewe lading in Nagaoka se " Saturnusmodel" in 'n sentrale kern gekonsentreer wat die elektrone in sirkelbane trek wat aan die ringe van Saturnus herinner. Min mense het destyds kennis geneem van die werk van Nagaoka,[16] en Nagaoka het selfs tydens die opvatting daarvan 'n fundamentele gebrek in die teorie erken, naamlik dat 'n klassieke gelaaide voorwerp nie orbitale beweging kan volhou nie omdat dit versnel en dus energie verloor deur elektromagnetiese bestraling.[12] Desondanks blyk dit dat die Saturnusmodel meer in gemeen het met die moderne teorie as enige van sy tydsgenote.

Die Bohr-atoom

wysig
 
Die Rutherford–Bohr-model van die waterstofatoom

In 1909 het Ernest Rutherford ontdek dat die grootste deel van die atoommassa in 'n kern gekondenseer is, wat ook positief gelaai is. Uit sy ontleding in 1911 het dit duidelik geword dat die pruimpoedingmodel nie die atoomstruktuur kon verklaar nie. In 1913 het Rutherford se postdoktorale student, Niels Bohr, 'n nuwe model van die atoom voorgestel, waarin elektrone in die klassieke wentelbane om die kern wentel, maar slegs toegelaat is om diskrete waardes van momentum te hê, gekwantifiseer in eenhede van h/2π[11] en hierdie beperking het outomaties slegs sekere waardes van elektronenergieë toegelaat. Die Bohr-model van die atoom het die probleem van energieverlies as gevolg van bestraling van 'n grondtoestand opgelos en het die oorsprong van spektrale lyne verduidelik.

Na Bohr se gebruik van Einstein se verduideliking van die foto-elektriese effek om energievlakke in atome in verband te bring met die golflengte van uitgestraalde lig, het die verband tussen die struktuur van elektrone in atome en die emissie- en absorpsiespektra van atome 'n al hoe nuttiger instrument geword in die begrip van elektrone in atome. Die mees opvallende kenmerk van emissie- en absorpsiespektra (eksperimenteel bekend sedert die middel van die 19de eeu ) was dat hierdie atoomspektra diskrete lyne bevat. Die belang van die Bohr-model was dat dit die lyne in emissie- en absorpsiespektra in verband gebring het met die energieverskille tussen die wentelbane wat elektrone rondom 'n atoom kon neem. Dit is egter nie deur Bohr bereik deur die elektrone 'n soort golfagtige eienskappe te gee nie, aangesien die idee dat elektrone kan optree as materiegolwe eers elf jaar later voorgestel is. Die Bohr-model se gebruik van gekwantifiseerde hoekmomenta en dus gekwantifiseerde energievlakke was egter 'n belangrike stap in die rigting van die begrip van elektrone in atome, en ook 'n belangrike stap in die rigting van die ontwikkeling van kwantummeganika, wat daarop dui dat gekwantifiseerde beperkings alle vir beide diskontinue energievlakke en spektra in atome moet verreken.

Met Franse fisikus Louis de Broglie se voorsteling oor die bestaan ​​van elektronmateriaalgolwe in 1924, en vir 'n kort tydjie voor die volledige Schrödinger-vergelyking in 1926 vir 'n waterstofagtige atoom, kon 'n Bohr-elektron "golflengte" gesien word as 'n funksie van sy momentum, en dus kan gesien word dat 'n elektron wat in 'n wentelbaan in 'n sirkel wentel op 'n veelvoud van sy halfgolflengte. Die Bohr-model kon vir 'n kort tydjie gesien word as 'n klassieke model met 'n bykomende beperking deur die "golflengte"-argument. Hierdie periode is egter onmiddellik vervang deur die volledige driedimensionele golfmeganika van 1926. In ons huidige begrip van fisika word die Bohr-model 'n "semi-klassieke model" genoem vanweë die kwantisering van die hoekmomentum en nie hoofsaaklik as gevolg van sy verhouding met elektrongolflengte, wa 'n dosyn jaar nadat die Bohr-model voorgestel is verskyn het.

Die Bohr-model kon die emissie- en absorpsiespektra van waterstof verklaar met die energieë van elektrone in die n = 1, 2, 3, ens. toestande in die Bohr-model wat ooreen stem met die van die huidige fisika. Dit het egter nie die ooreenkomste tussen verskillende atome, soos uitgedruk in die periodieke tabel, verklaar nie, soos die feit dat helium (twee elektrone), neon (10 elektrone) en argon (18 elektrone) soortgelyke chemiese "traagheid" vertoon. Moderne kwantummeganika verklaar dit aan die hand van elektronskulpe en subdoppe wat elk 'n aantal elektrone kan bevat wat bepaal word deur die uitsluitingsbeginsel van Pauli. Dus kan die n = 1-toestand een of twee elektrone bevat, terwyl die n = 2-toestand tot agt elektrone in 2s en 2p-subdoppe kan hou. In helium is alle n = 1 toestande volledig beset; dieselfde geld vir n = 1 en n = 2 in neon. In argon word die 3s en 3p-subdoppe volledig beset deur agt elektrone; kwantummeganika laat ook 'n 3d-subdop toe, maar dit is op hoër energie as die 3s en 3p in argon (in teenstelling met die situasie in die waterstofatoom) en bly leeg.

Moderne opvattings en verbindings met die onsekerheidsbeginsel van Heisenberg

wysig

Onmiddellik nadat Duitse fisikus Werner Heisenberg sy onsekerheidsbeginsel ontdek het,[17] het Bohr opgemerk dat die bestaan ​​van enige soort "golfpakket" onsekerheid in die golffrekwensie en golflengte impliseer, aangesien 'n verspreiding van frekwensies nodig is om die pakket self te skep.[18] In kwantummeganika, waar alle partikelmomentas met golwe geassosieer word, is dit die vorming van so 'n golfpakket wat die golf, en dus die deeltjie, in die ruimte lokaliseer. In state waar 'n kwantummeganiese deeltjie gebind is, moet dit as 'n golfpakket gelokaliseer word, en die bestaan ​​van die pakket en die minimum grootte daarvan impliseer 'n verspreiding en minimale waarde in die deeltjiegolflengte, en dus ook momentum en energie. In die kwantummeganika, aangesien 'n deeltjie in 'n kleiner gebied in die ruimte gelokaliseer is, benodig die gepaardgaande saamgeperste golfpakket 'n groter en groter spektrum van momenta, en dus groter kinetiese energie. Dus neem die bindingsenergie toe om 'n deeltjie in 'n kleiner ruimte te hou of te vang, sonder om te bind, namate die gebied van die ruimte kleiner word. Deeltjies kan nie beperk word tot 'n meetkundige punt in die ruimte nie, aangesien dit 'n oneindige groot deeltjie-momentum benodig.

In die chemie het Schrödinger, Pauling, Mulliken en andere opgemerk dat die gevolg van Heisenberg se verhouding was dat die elektron, as 'n golfpakket, nie as 'n presiese ligging in sy baan beskou kon word nie. Duitse fisikus Max Born het voorgestel dat die posisie van die elektron beskryf moet word deur 'n waarskynlikheidsverdeling wat verband hou met waar die elektron te vinde is op 'n stadium in die golffunksie wat die gepaardgaande golfpakket beskryf. Die nuwe kwantummeganika het nie presiese resultate gegee nie, maar slegs die waarskynlikheid vir die voorkoms van 'n verskeidenheid moontlike sulke resultate. Heisenberg was van mening dat die baan van 'n bewegende deeltjie geen betekenis het as ons dit nie kan waarneem nie, soos ons dit nie met elektrone in 'n atoom kan doen nie.

Orbitale energie

wysig

In atome met 'n enkele elektron ('n waterstofagtige atoom) word die energie van 'n baan (en gevolglik van enige elektrone in die baan) hoofsaaklik bepaal deur n. Die orbitaal n = 1 het die laagste moontlike energie in die atoom. Elke opeenvolgende hoër waarde van n het 'n hoër vlak van energie, maar die verskil neem af namate n toeneem. Vir hoë n word die energievlak so hoog dat die elektron maklik uit die atoom kan ontsnap.

In atome met veelvuldige elektrone hang die energie van 'n elektron nie net af van die intrinsieke eienskappe van sy baan nie, maar ook van die interaksie daarvan met die ander elektrone. Hierdie interaksies word ook deur die besonderhede van die ruimtelike waarskynlikheidsverdeling daarvan verander, en dus is die energievlakke van orbitale nie net van n afhanklik nie, maar ook van ℓ. Hoër waardes van ℓ word geassosieer met hoër energiewaardes; byvoorbeeld, die 2p-toestand is hoër as die 2s-toestand. Wanneer ℓ = 2, word die toename in energie van die baan so groot dat dit die energie van die orbitaal bo die energie van die s-orbitaal in die volgende hoër dop druk; wanneer ℓ = 3 word die energie twee trappe hoër in die dop gedruk. Byvoorbeeld, die vulling van die 3d-orbitale vind eers plaas as die 4s-orbitale gevul is. Dit het tot gevolg dat die subdoppe in die volgende volgorde gevul word: 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p, ens.

Hierdie gedrag is verantwoordelik vir die struktuur van die periodieke tabel. Die eerste twee kolomme aan die linkerkant is die s-blok, die laaste drie kolomme aan die regterkant die p-blok en die d- en f-blokke in die middel.

Kwantumeffekte

wysig

Relatiwistiese effekte

wysig

Vir elemente met 'n hoë atoomgetal Z word die effekte van relatiwiteit meer opvallend, en veral ook vir die s-elektrone, wat teen relativistiese snelhede beweeg as hulle die siftingselektrone binnedring naby die kern van atome met hoë Z-nommer. Hierdie relativistiese toename in momentum vir hoëspoed-elektrone veroorsaak 'n ooreenstemmende afname in golflengte en inkrimping van die 6s-orbitale relatief tot die 5d-orbitale (in vergelyking met ooreenstemmende s- en d-elektrone in ligter elemente in dieselfde kolom van die periodieke tabel) en dit lei daartoe dat 6s valenselektrone in energie verlaag word.

Voorbeelde van beduidende fisiese uitkomste van hierdie effek sluit in die verlaagde smelttemperatuur van kwik (wat die gevolg is van 6s-elektrone wat nie beskikbaar is vir metaalbinding nie) en die goue kleur van goud en sesium.[19]

Oorgange tussen orbitale

wysig

Gebonde kwantumtoestande het afsonderlike energievlakke wat beteken dat die energieverskille tussen toestande in atoomorbitale ook afsonderlik is. 'n Oorgang tussen hierdie toestande (dws 'n elektron wat 'n foton absorbeer of uitstraal) kan dus slegs gebeur as die foton 'n energie het wat ooreenstem met die presiese energieverskil tussen genoemde toestande.

Dit beteken verder dat vir 'n elektron om van een energietoestand in 'n atoom in 'n ander te beweeg, dit die verskil in energie tussen die twee toestande presies moet verkry of verloor. In 'n straal multi-frekwensie-lig sou die fotone met die regte hoeveelheid energie deur die atoom geabsorbeer word om van toestand te verander en sodoende 'n donker lyn (of absorbsielyn) in die spektrum veroorsaak. As die elektron energie sou uitstraal terwyl dit van 'n hoë energietoestand na 'n laer energietoestand beweeg, kon dit slegs fotone van 'n spesifieke golflengte afgee op grond van die verskil in energie tussen die toestande. Dit sou 'n emissie-spektrum wees. Eksperimentele metings van sowel absorpsie- as emissiespektra is deel van die validering van die atoomorbitaalmodel.

Verwysings

wysig
  1. ↑ Orchin, Milton; Macomber, Roger S.; Pinhas, Allan; Wilson, R. Marshall (2005). Atomic Orbital Theory (PDF) (in Engels).
  2. ↑ Daintith, J. (2004). Oxford Dictionary of Chemistry (in Engels). New York: Oxford University Press. ISBN 978-0-19-860918-6.
  3. ↑ Griffiths, David (1995). Introduction to Quantum Mechanics (in Engels). Prentice Hall. pp. 190–191. ISBN 978-0-13-124405-4.
  4. ↑ Levine, Ira (2000). Quantum Chemistry (in Engels) (5 uitg.). Prentice Hall. p. 144. ISBN 978-0-13-685512-5.
  5. ↑ Laidler, Keith J.; Meiser, John H. (1982). Physical Chemistry (in Engels). Benjamin/Cummings. p. 488. ISBN 978-0-8053-5682-3.
  6. ↑ Atkins, Peter; de Paula, Julio; Friedman, Ronald (2009). Quanta, Matter, and Change: A Molecular Approach to Physical Chemistry (in Engels). Oxford University Press. p. 106. ISBN 978-0-19-920606-3.
  7. ↑ Feynman, Richard; Leighton, Robert B.; Sands, Matthew (2006). The Feynman Lectures on Physics -The Definitive Edition, Vol 1 lect 6 (in Engels). Pearson PLC, Addison Wesley. p. 11. ISBN 978-0-8053-9046-9.
  8. ↑ Slater, J. C. (1930). "Atomic Shielding Constants". Physical Review (in Engels). 36 (1): 57. Bibcode:1930PhRv...36...57S. doi:10.1103/PhysRev.36.57.
  9. ↑ Gill, Peter M.W. (1994). "Molecular integrals Over Gaussian Basis Functions" (PDF). Advances in Quantum Chemistry (in Engels). 25: 141–205. Bibcode:1994AdQC...25..141G. doi:10.1016/S0065-3276(08)60019-2. ISBN 9780120348251. Besoek op 23 Oktober 2020.
  10. ↑ Mulliken, Robert S. (Julie 1932). "Electronic Structures of Polyatomic Molecules and Valence. II. General Considerations". Physical Review (in Engels). 41 (1): 49–71. Bibcode:1932PhRv...41...49M. doi:10.1103/PhysRev.41.49.
  11. ↑ 11,0 11,1 Bohr, Niels (1913). "On the Constitution of Atoms and Molecules". Philosophical Magazine (in Engels). 26 (1): 476. Bibcode:1914Natur..93..268N. doi:10.1038/093268a0. S2CID 3977652.
  12. ↑ 12,0 12,1 12,2 Nagaoka, Hantaro (Mei 1904). "Kinetics of a System of Particles illustrating the Line and the Band Spectrum and the Phenomena of Radioactivity". Philosophical Magazine (in Engels). 7 (41): 445–455. doi:10.1080/14786440409463141. Geargiveer vanaf die oorspronklike op 27 November 2017. Besoek op 23 Oktober 2020.
  13. ↑ Bryson, Bill (2003). A Short History of Nearly Everything (in Engels). Broadway Books. pp. 141–143. ISBN 978-0-7679-0818-4.
  14. ↑ Thomson, J. J. (1897). "Cathode rays". Philosophical Magazine (in Engels). 44 (269): 293. doi:10.1080/14786449708621070.
  15. ↑ Thomson, J. J. (1904). "On the Structure of the Atom: an Investigation of the Stability and Periods of Oscillation of a number of Corpuscles arranged at equal intervals around the Circumference of a Circle; with Application of the Results to the Theory of Atomic Structure" (uittreksel van 'n papier). Philosophical Magazine. Series 6 (in Engels). 7 (39): 237–265. doi:10.1080/14786440409463107.
  16. ↑ Rhodes, Richard (1995). The Making of the Atomic Bomb (in Engels). Simon & Schuster. pp. 50–51. ISBN 978-0-684-81378-3.
  17. ↑ Heisenberg, W. (Maart 1927). "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik (Afr: Oor die beskrywende inhoud van kwantumteoretiese kinematika en meganika)". Zeitschrift für Physik A (in Duits). 43 (3–4): 172–198. Bibcode:1927ZPhy...43..172H. doi:10.1007/BF01397280. S2CID 122763326.
  18. ↑ Bohr, Niels (April 1928). "The Quantum Postulate and the Recent Development of Atomic Theory". Nature (in Engels). 121 (3050): 580–590. Bibcode:1928Natur.121..580B. doi:10.1038/121580a0.
  19. ↑ Lower, Stephen. "Primer on Quantum Theory of the Atom".
Ontsluit van "https://af.wikipedia.org/w/index.php?title=Atoomorbitaal&oldid=2700874"