Fermat se reghoekigedriehoekstelling

Hierdie artikel moet skoongemaak of andersins verbeter word. Hierdie artikel voldoen nie tans aan die hoë gehaltestandaarde waarna Wikipedia streef nie. Voel vry om self in te spring en verbeterings te maak, en verwyder hierdie kennisgewing ná die tyd. Vir meer hulp, sien die redigeringshulp. Daar is moontlik kommentaar in die artikel of op die besprekingsblad oor wat verbeter moet word.

Fermat se reghoekigedriehoekstelling is 'n nie-bestaan bewys in die getalteorie, die enigste volledige bewys wat deur Pierre de Fermat nagelaat is. Dit het verskeie ekwivalente formulerings:

• As drie vierkante getalle 'n rekenkundige progressie vorm, kan die gaping tussen opeenvolgende getalle in die progressie ('n kongruum genoem) nie self vierkantig wees nie.
• Daar bestaan nie twee Pythagorea driehoeke waarin die twee bene van een driehoek die been en skuinssy van die ander driehoek is nie.
• 'n Reghoekige driehoek waarvoor al drie sylengtes rasionale getalle is, kan nie 'n area hê wat die vierkant van 'n rasionale getal is nie. 'n Gebied wat op hierdie manier gedefinieer word, word 'n kongruente getal genoem, en geen kongruente getal kan dus vierkantig wees nie.
• 'n Reghoekige driehoek en 'n vierkant met gelyke gebiede kan nie alle kante met mekaar ooreenstem nie.
• Die enigste rasionale punte op die elliptiese kromme $y^{2}=x(x-1)(x+1)$ is die drie triviale punte (0,0), (1,0) en (-1,0).
• Die Diofantynvergelyking $x^{4}-y^{4}=z^{2}$ het geen heelgetaloplossing nie.

Twee reghoekige driehoeke met die twee kante van die boonste een wat gelyk is aan die sy en die skuinssy van die onderste een. Volgens Fermat se reghoekigedriehoekstelling is dit nie moontlik vir al vier lengtes a, b, c en d om heelgetalle te wees nie.

'n Onmiddellike gevolg van die laaste van hierdie formulerings is dat Fermat se laaste stelling waar is vir die eksponent n = 4.

Formulering

Vierkante in rekenkundige vordering

In 1225 is Fibonacci uitgedaag om 'n konstruksie te vind vir drievoudige kwadraatgetalle wat eweredig van mekaar afgestrek is, 'n rekenkundige vordering vorm en vir die spasiëring tussen hierdie getalle, wat hy 'n kongruum genoem het. Een manier om Fibonacci se oplossing te beskryf is dat die getalle wat gekwadrateer moet word, die verskil is van bene, skuinssy en som van bene van 'n Pythagoreaanse driehoek en dat die kongruum vier keer die oppervlakte van dieselfde driehoek is. In sy latere werk oor die kongruumprobleem, gepubliseer in Die Boek van Kwadrate, het Fibonacci opgemerk dat dit onmoontlik is vir 'n kongruum om self 'n kwadraatgetal te wees, maar het nie 'n bevredigende bewys van hierdie feit voorgelê nie.

As drie kwadrate $a^{2}$, $b^{2}$, en $c^{2}$ 'n rekenkundige vordering kon vorm waarvan die kongruum ook 'n vierkant $d^{2}$ was, dan sou hierdie getalle die Diophantynse vergelykings bevredig

$a^{2}+d^{2}=b^{2}$ en $b^{2}+d^{2}=c^{2}$.

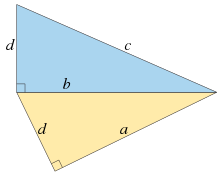
Dit wil sê, volgens die Pythagorese stelling, sou hulle twee heelgetal reghoekige driehoeke vorm waarin die paar $(d,b)$ een been en die skuinssy van die kleiner driehoek gee en dieselfde paar vorm ook die twee bene van die groter driehoek. Maar as (soos Fibonacci beweer het) geen kwadraatkongruum kan bestaan nie, dan kan daar geen twee heelgetalle reghoekige driehoeke wees wat op hierdie manier twee kante deel nie.

Gebiede van regte driehoeke

Aangesien die kongrua presies die getalle is wat vier keer die gebied van 'n Pythagorese driehoek is, en aangesien vermenigvuldiging met vier nie verander of 'n getal vierkantig is nie, is die bestaan van 'n kwadraatkongruum gelykstaande aan die bestaan van 'n Pythagorese driehoek met 'n vierkantige area. Dit is hierdie variant van die probleem wat Fermat se bewys betref: hy toon dat daar nie so 'n driehoek is nie. By die oorweging van hierdie probleem is Fermat nie deur Fibonacci geïnspireer nie, maar deur 'n uitgawe van Diophantus gepubliseer deur Claude Gaspard Bachet de Méziriac. Hierdie boek beskryf verskeie spesiale reghoekige driehoeke waarvan die gebiede vorms het wat verband hou met vierkante, maar het nie die geval van gebiede wat hulself kwadreer oorweeg nie.

Deur die vergelykings vir die twee Pythagorese driehoeke hierbo te herrangskik, en dan saam te vermenigvuldig, kry mens die enkeldiophantiese vergelyking

$b^{4}-d^{4}=(b^{2}-d^{2})(b^{2}+d^{2})=a^{2}c^{2}$

wat kan vereenvoudig word 

$b^{4}-d^{4}=e^{2}.$

Omgekeerd kan enige oplossing vir hierdie vergelyking in berekening gebring word om 'n vierkante kongruum te gee. Die oplosbaarheid van hierdie vergelyking is dus gelyk aan die bestaan van 'n vierkante kongruum. Maar, as Fermat se laaste stelling vals was vir die eksponent $n=4$, dan sal een van die drie getalle in enige teenvoorbeeld ook vier getalle gee wat hierdie vergelyking oplos. Daarom impliseer Fermat se bewys dat geen Pythagorese driehoek 'n vierkantige area het nie, dat hierdie vergelyking geen oplossing het nie en dat hierdie geval van Fermat se laaste stelling waar is.

Nog 'n ekwivalente formulering van dieselfde probleem behels kongruente getalle, die getalle wat gebiede van reghoekige driehoeke is waarvan die drie kante al rasionale getalle is. Deur die kante van 'n gemeenskaplike noemer te vermenigvuldig, kan enige kongruente getal in die gebied van 'n Pythagorese driehoek omskep word, waaruit volg dat die kongruente getalle presies die getalle is wat gevorm word deur 'n kongruum te vermenigvuldig met die vierkant van 'n rasionale getal. Daar is dus geen vierkante kongruum as en slegs as die getal 1 nie 'n kongruente getal is nie. Ekwivalent is dit onmoontlik vir 'n vierkant (die geometriese vorm) en 'n reghoekige driehoek om beide gelyke areas en alle sye in ooreenstemming met mekaar te hê.

Elliptiese kurwe

Nog 'n soortgelyke vorm van Fermat se stelling behels die elliptiese kromme wat bestaan uit die punte waarvan die Cartesiese koördinate $(x,y)$ die vergelyking bevredig

$y^{2}=x(x+1)(x-1).$

Hierdie vergelyking het die ooglopende pare oplossings (0,0), (1,0) en (-1,0). Fermat se stelling is gelykstaande aan die stelling dat dit die enigste punte op die kromme is waarvoor beide x en y rasioneel is.

Fermat se bewys

Gedurende sy leeftyd het Fermat verskeie ander wiskundiges uitgedaag om die nie-bestaan van 'n Pythagorese driehoek met vierkantige oppervlak te bewys, maar het nie die bewys self gepubliseer nie. Hy het egter 'n bewys in sy kopie van Bachet se Diophantus geskryf, wat sy seun postuum ontdek en gepubliseer het.

Fermat se bewys is 'n bewys deur oneindige afkoms. Dit toon aan dat, uit enige voorbeeld van 'n Pythagoreaanse driehoek met vierkantige area, 'n kleiner voorbeeld kan ontstaan. Aangesien Pythagorese driehoeke positiewe heelgetaloppervlaktes het, en daar nie 'n oneindige afnemende volgorde van positiewe heelgetalle bestaan nie, kan daar ook nie 'n Pythagorese driehoek met vierkantige oppervlakte bestaan nie.

Veronderstel in meer detail dat x, y en z die heelgetalle van 'n regte driehoek met vierkantige oppervlakte is. Deur te verdeel deur enige algemene faktore, kan 'n mens aanvaar dat hierdie driehoek primitief is en uit die bekende vorm van alle primitiewe Pythagorea-driedubbels, kan mens x = 2pq, y = p ^ {2} -q ^ {2} stel en z = P ^ {2} + q ^ {2}, waardeur die probleem getransformeer word om relatief prima heelgetalle p en q te vind (een daarvan is ewe) sodat pq (p ^ {2} -q ^ {2}) vierkante is. Die vier lineêre faktore p, q, p + q, en p-q is relatief prima en moet dus self vierkante wees; Laat p + q = r ^ {2} en p-q = s ^ {2}. Beide r en s moet vreemd wees aangesien presies een van p of q ewe is en die ander een is vreemd. Daarom is beide (rs) en (r + s) selfs, waarvan een deelbaar is met 4. Uit hierdie twee getalle ontleen Fermat nog twee getalle u = (rs) / 2 en v = (r + s) / 2, een daarvan is selfs in die vorige sin. Omdat u ^ {2} + v ^ {2} = p 'n vierkant is, is u en v die bene van 'n ander primitiewe Pythagoreaanse driehoek waarvan die area (uv) / 2 = q / 4. Aangesien q self 'n vierkant is en aangesien uv selfs is, is q / 4 'n vierkant. So, 'n Pythagorasiese driehoek met vierkantige area lei tot 'n kleiner Pythagoreaanse driehoek met vierkantige oppervlakte, wat die bewyse voltooi.